We often encounter the challenge of finding efficient algorithms to solve problems. One such problem is finding a continuous sub-sequence with maximum sum in an array. The sliding window algorithm is a well-known technique used to solve this problem efficiently. In this article, we will take a closer look at what sliding window algorithm is, how it works and its applications.
What is the Sliding Window Algorithm? The sliding window algorithm is a technique that is used to solve problems that require analyzing a sequence of elements in a given array, where the objective is to find the maximum sum of a continuous sub-sequence within the array. It operates by maintaining a window of elements and continuously moving it to cover all the elements of the array.
How does it work? The sliding window algorithm operates by maintaining a window of elements in the array and continuously moving it to cover all the elements of the array. It starts with a window of a specified size, and then continuously slides the window to the right by one element. At each step, the algorithm calculates the sum of the elements within the window and compares it to the maximum sum found so far. If the sum is greater, it updates the maximum sum.
Lets understand with an example:
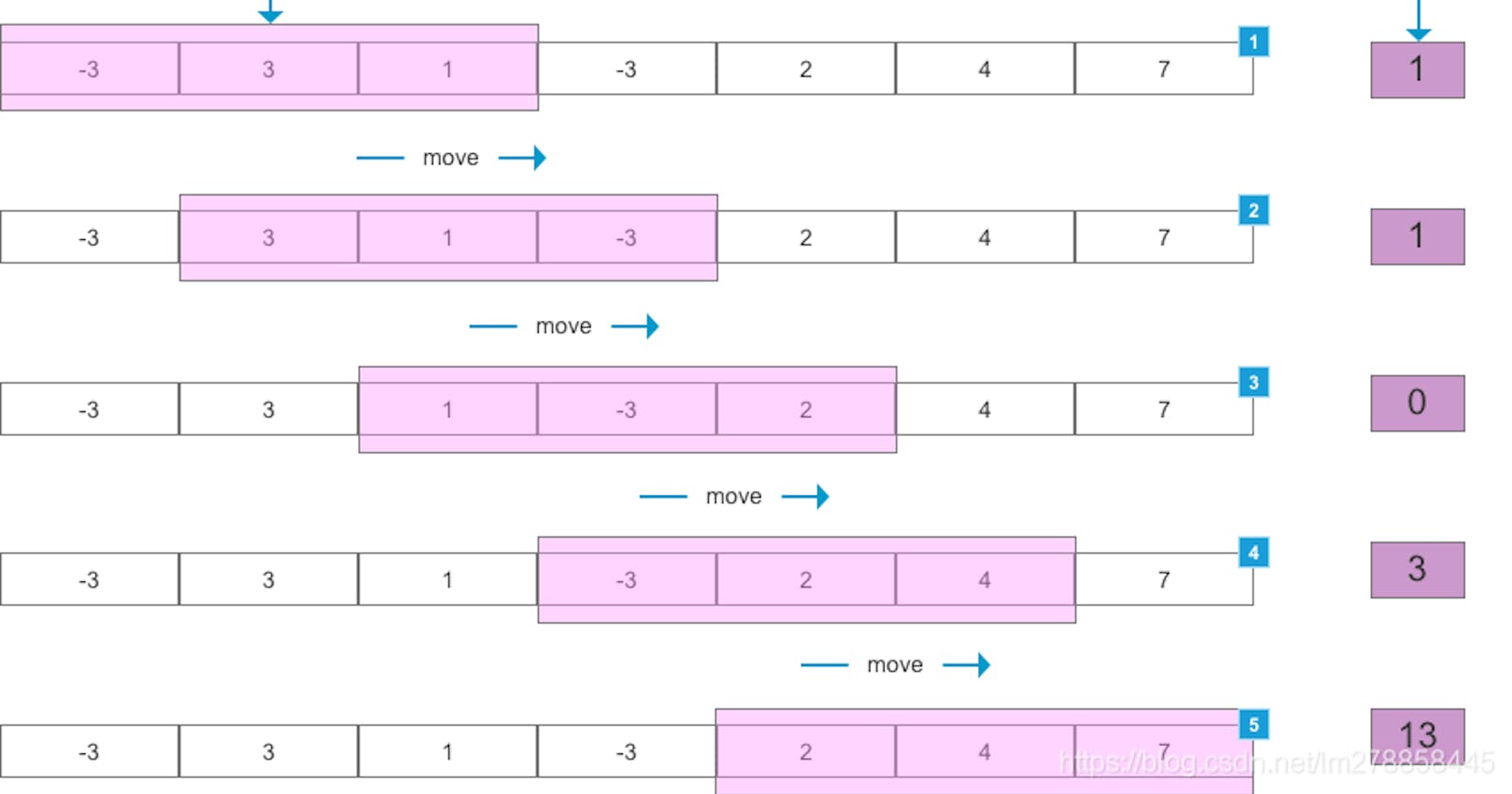
Consider an array of integers: [4, 2, 5, 1, 7, 3, 6, 2] and the size of the sliding window is 3.
Start with the first 3 elements
[4, 2, 5]and calculate their sum, which is11.Slide the window by one element to the right, the new window becomes
[2, 5, 1]and the sum is8.Slide the window again to the right, the new window becomes
[5, 1, 7]and the sum is13.Continue sliding the window to the right until it reaches the end of the array.
The maximum sum of a continuous sub-sequence is
13, which is obtained from the window[5, 1, 7].
The algorithm provides an efficient solution with a time complexity of O(n), making it a fast and reliable solution for solving this problem.
Here's an example of how you can implement the sliding window algorithm in C++ to find the maximum sum of a continuous sub-sequence in an array.
#include<iostream>
#include<vector>
using namespace std;
int maxSum(vector<int>& nums, int k) {
int max_sum = 0;
int window_sum = 0;
for(int i = 0; i < k; i++) {
window_sum += nums[i];
}
max_sum = window_sum;
for(int i = k; i < nums.size(); i++) {
window_sum += nums[i] - nums[i-k];
max_sum = max(max_sum, window_sum);
}
return max_sum;
}
int main() {
vector<int> nums = {1,2,3,4,5};
int k = 3;
cout<<"Maximum sum of a continuous sub-sequence: "<<maxSum(nums, k)<<endl;
return 0;
}
In the above code, the maxSum function takes an array of integers and an integer k as input. The function initializes the window_sum with the sum of the first k elements of the array and stores the result in max_sum. Then it slides the window by one element and updates the window_sum and max_sum at each step. The function returns the maximum sum of a continuous sub-sequence in the array.
The main function creates an example array nums and calls the maxSum function with the array and an integer k as input. The function returns the maximum sum of a continuous sub-sequence in the array, which is printed out in the console.
Applications of the Sliding Window Algorithm The sliding window algorithm can be used in a variety of applications, including:
Finding the maximum sum of a continuous sub-sequence in an array.
Optimizing the time complexity of string matching algorithms.
Real-time data processing, such as in streaming data analytics.
Conclusion In conclusion, the sliding window algorithm is a technique that is widely used in various areas of computer science, including algorithms, data structures and real-time data processing. It provides an efficient solution to the problem of finding the maximum sum of a continuous sub-sequence in an array, and has a time complexity of O(n), making it a fast and reliable solution. If you're facing a similar problem in your software engineering projects, consider using the sliding window algorithm to optimize the time complexity and get the best results.